BC HEALTH
Saved by @CodyyyGardner

THREAD
I created a simple table to illustrate the individual impact of the "flexible second dose timing" now recommended in the UK.

Coincidentally, @bob_wachter & @ashishkjha just tackled the US policy question in this important piece. 1/
https://t.co/n5bHkdIo0c

 I based this on recent statements from the UK chief medical officers, JCVI, and what we know from prior vaccine development. 2/

JCVI: https://t.co/6FQ25d6MFE

UK Chief Medical Officer (CMO) statement: https://t.co/RTpAIqgE1i

CMO letter to the profession: https://t.co/4WeexrVYWX
This table and thread focuses on the AZ vaccine, where more data on a delayed second dose is available than with the Pfizer vaccine. It is not intended to address questions about single-dose regimens or mix & match approaches. 3/
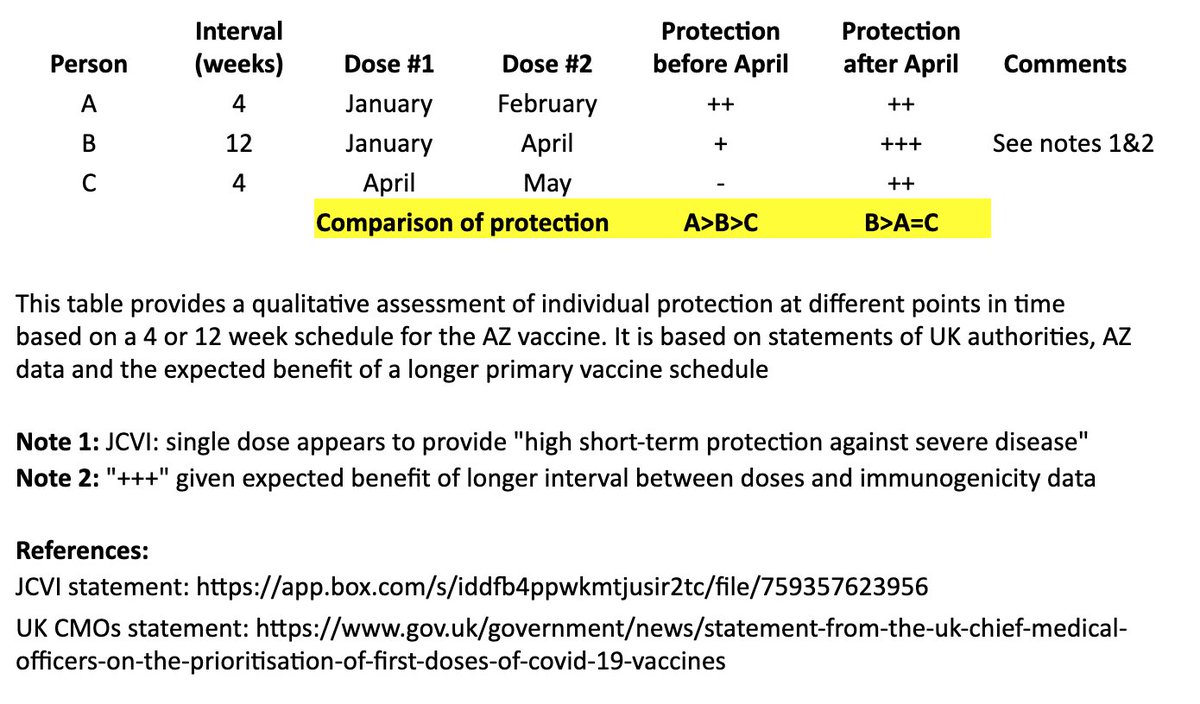
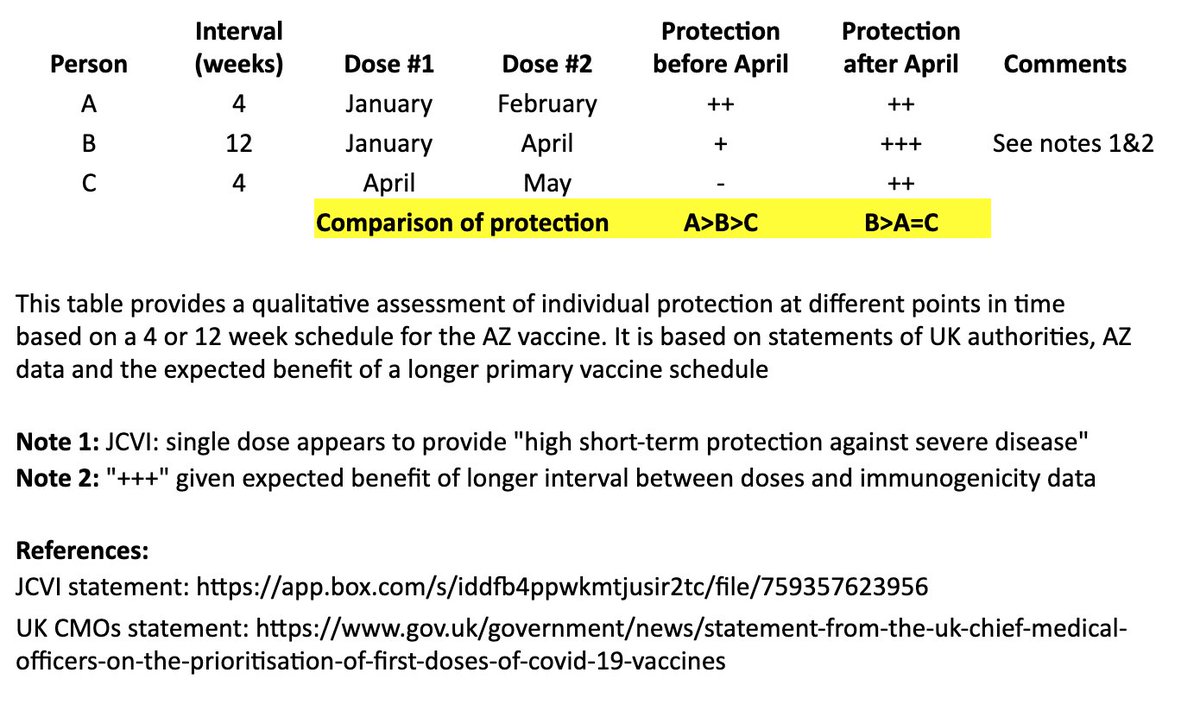
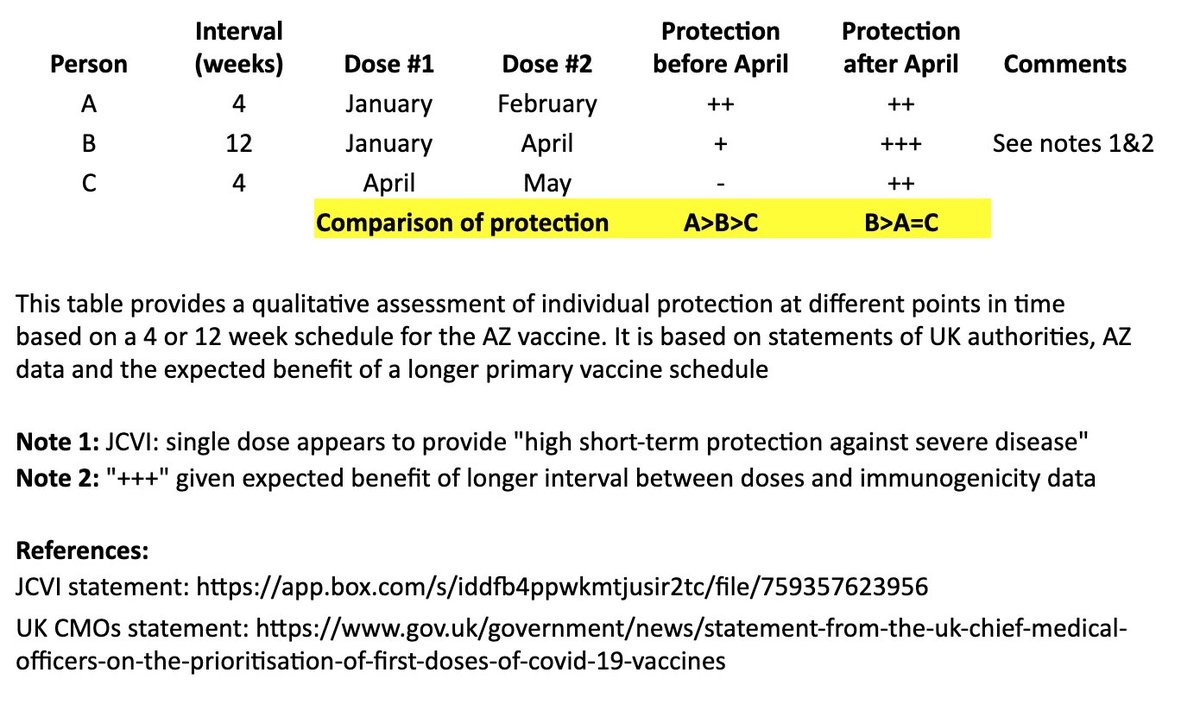
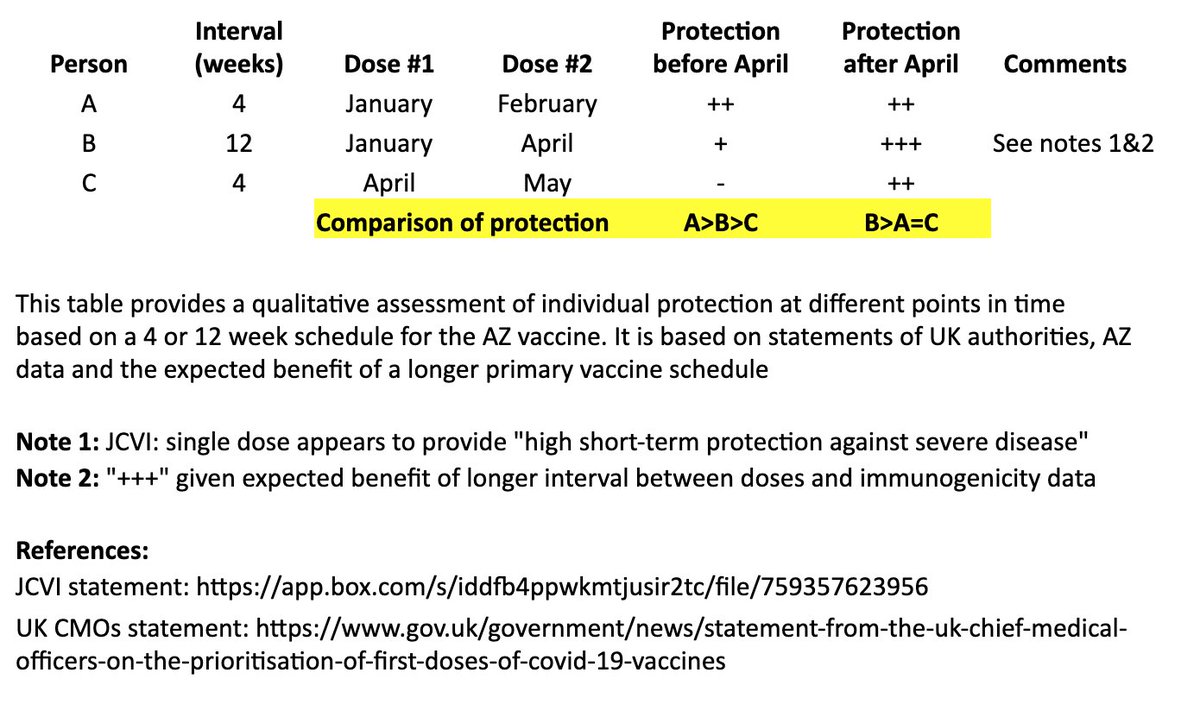
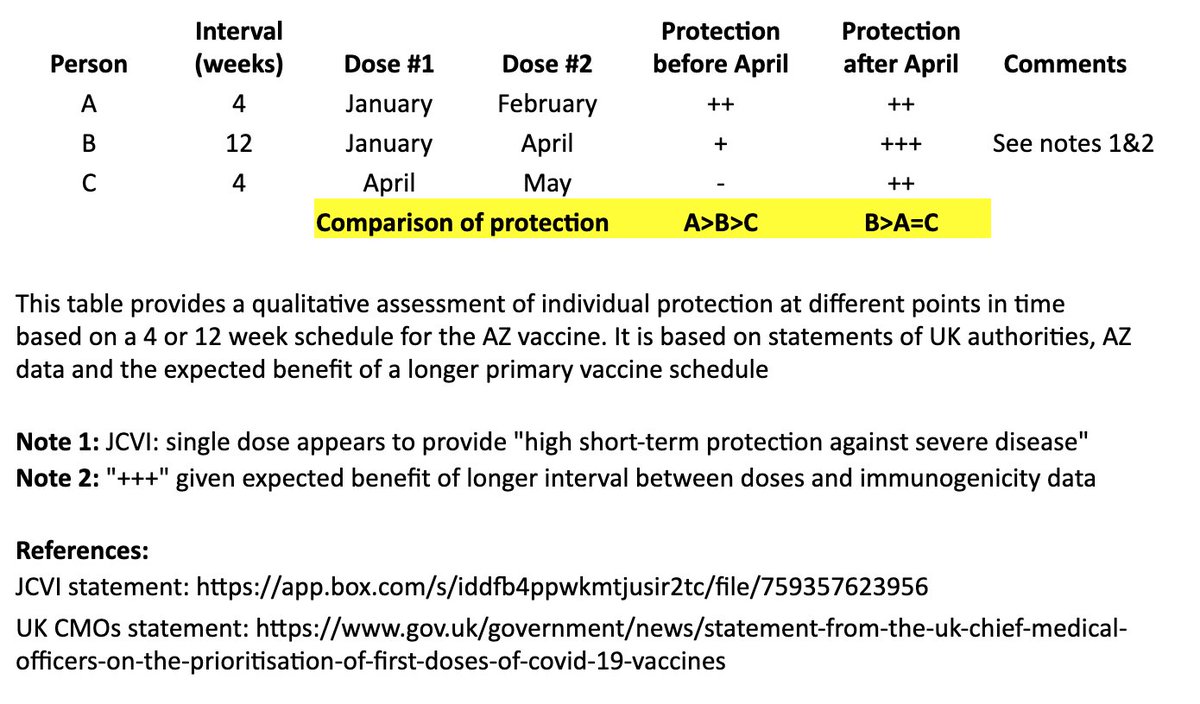
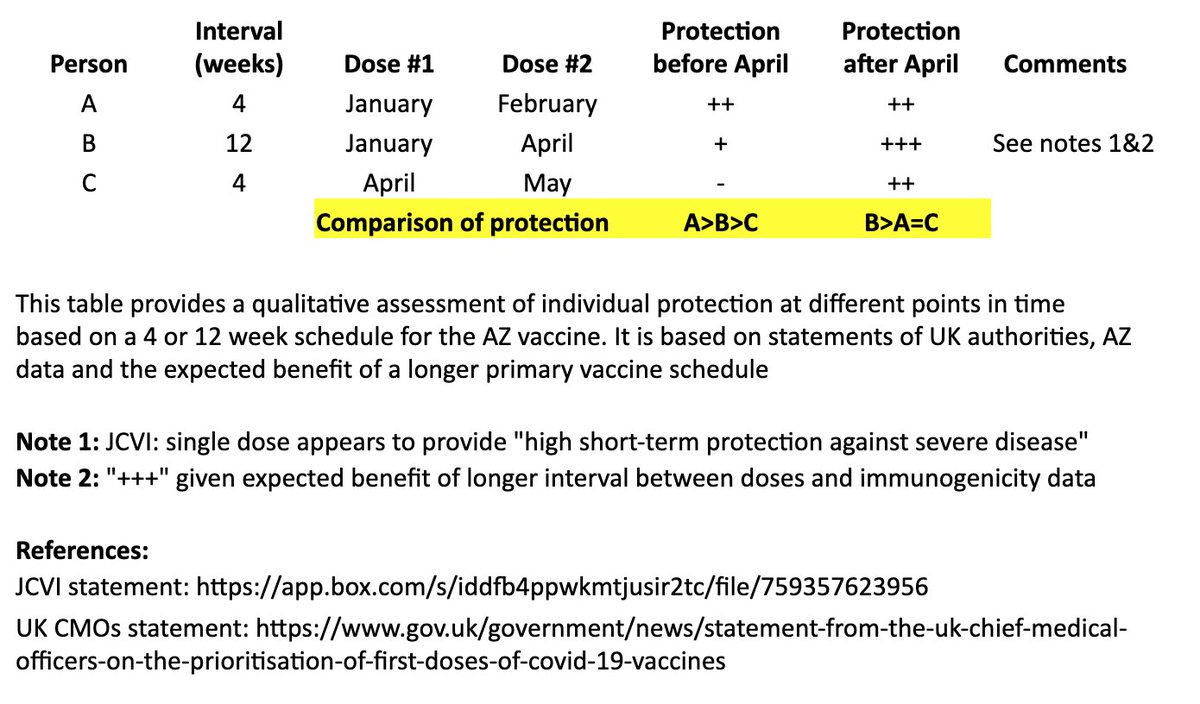
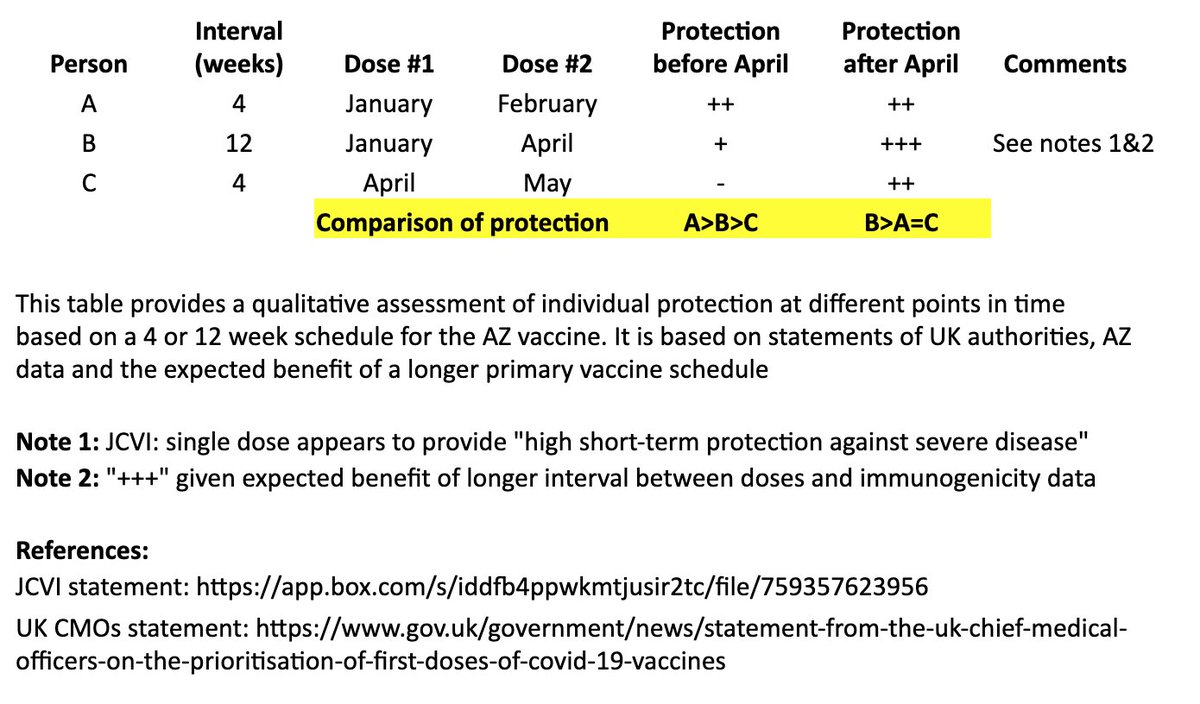
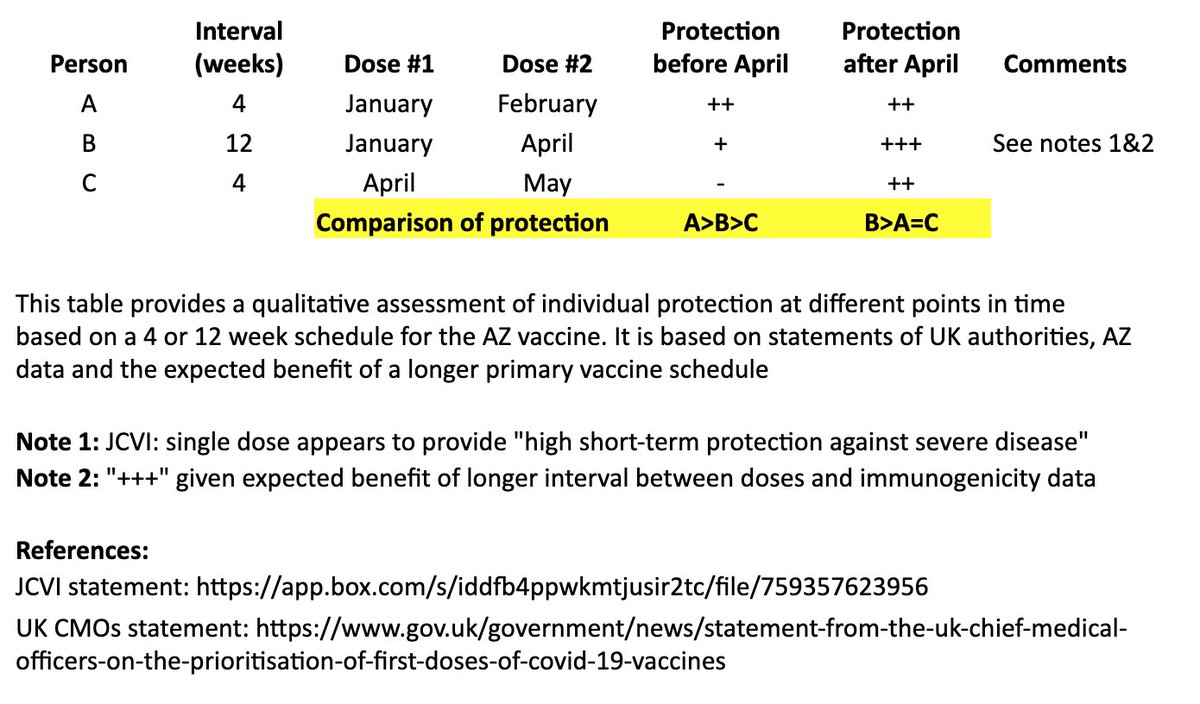
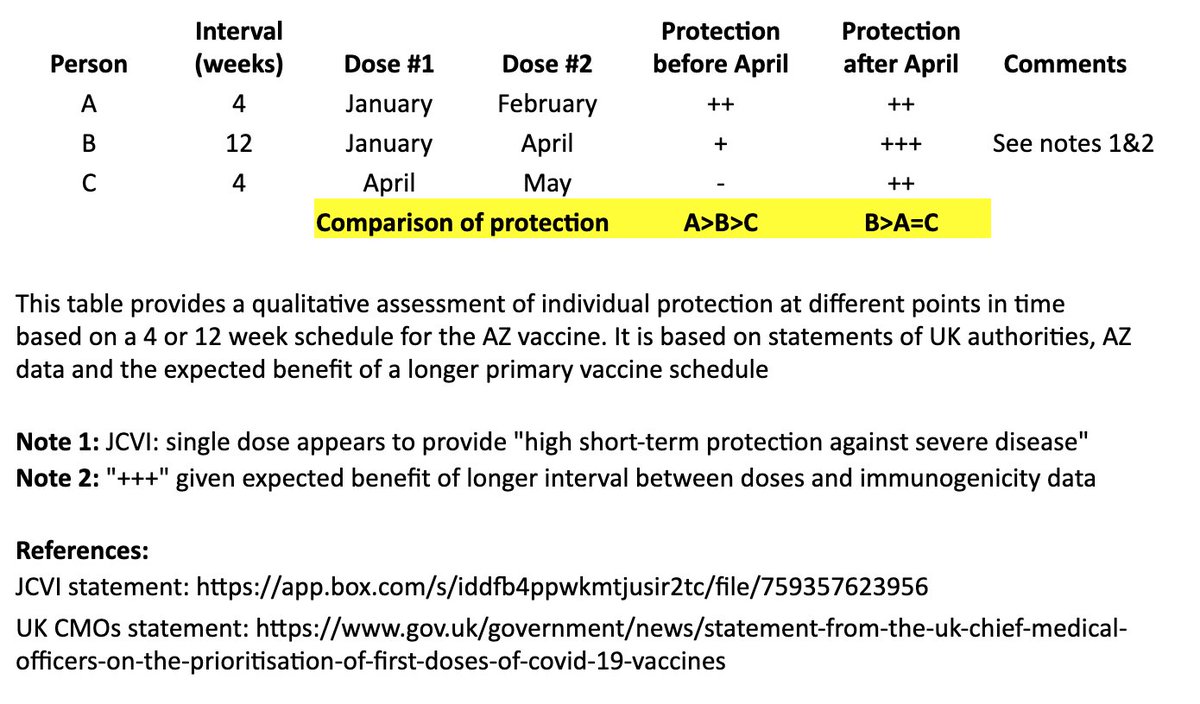
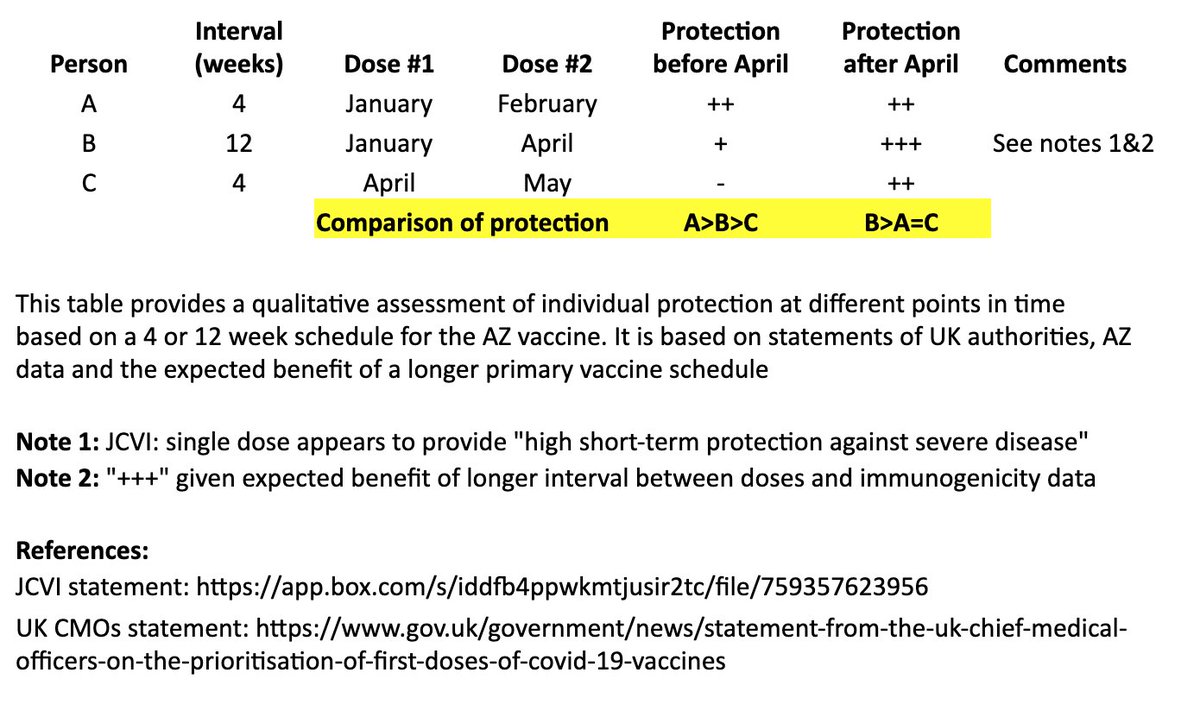
In the table, persons “A” and “B” both receive their first dose in January. “A” receives their second dose in February (4 weeks later), and “B” receives their second dose in April (12 weeks later). “C” receives their first dose in April and second dose in May (4 weeks later). 4/
I made a qualitative comparison the potential efficacy during the two months between “A” and “B’s” second dose, as well as the potential longer-term efficacy after “B” receives their second dose. 5/
For the two-month period between the timing of “A” and “B’s” second dose, the level of protection for “A” may be greater than “B,” as “A” has received their second dose, although JCVI suggests that most of this early protection is provided by the first dose. 6/
JCVI says first-dose protection against hospitalization is high, so for that two month interval, I’ve assumed “B” is expected to be protected against the more severe forms of COVID-19 (“+”). 7/
After “B’s” second dose in April, we expect a more robust, higher quality and longer-lasting immune response than “A,” as is often seen with longer intervals in a primary vaccination series and supported by AZ’s data immunogenicity data. 8/
https://t.co/cqKIpomUHg
The bottom line is that “A” may see some protective benefit over “B” for two months (although “B” is expected to be protected against severe COVID during that time), but “B” is expected to have better long-term protection after they receive their second dose at 12 weeks. 9/
In other words, for the two months between “A” and “B’s” second dose: A>B>C

For the longer term, after “B” receives their second dose: B>A=C

10/
At a population level, this strategy could double the number of people immunized immediately while production ramps up. Many in category “C” could shift to “B.”

This assumes immunization programs are keeping up with the number of doses available. 11/
A few important caveats: (1) the assumption of sustained efficacy after the first dose is based on an exploratory analysis in the age 18-55 population. This needs to be confirmed in the older adult population. Exploratory analyses have limitations, esp if not pre-specified. 12/
(2) the assumption that a longer schedule (“B”) will result in a higher-quality, more durable immune response is based on immunogenicity data and experience with other vaccines. The efficacy impact will have to be confirmed. 13/
(3) we need to confirm that vaccine protection against the new strain is comparable after the first and second doses, given the affinity maturation expected with a second dose. 14/
Some virologists have raised the theoretical concern that a change in schedule could promote emergence of vaccine escape mutants. This is an important consideration that has implications for single-dose vaccine development and WHO’s minimum vaccine efficacy threshold of 50%. 15/
Again, this illustration is based on statements from UK authorities, AZ’s published data, and what is known from prior vaccine development. It is not a prediction of the future or what will happen to any individual, and is subject to updates as new data becomes available. 16/
I hope this helps people understand the practical ramifications of the UK recommendations and the pros/cons at individual and population levels. The urgency of the question is driven by the emergence of the new variant in the UK as well as the limited supply of vaccine. 17/
Thanks to our vaccine CMO, Dr. Gary Dubin for his input. More thoughts and links to others' views in the thread below.

I went through this exercise to clarify my own views and thought others might find it useful. Please take it in that spirit! 18/ https://t.co/2vzJ9Sdfc4

More from Health

\u2744\ufe0fI'm A Fuckin' Princess\u2744\ufe0f
❄️I'm A Fuckin' Prince...
@Just_ReneaR
I'm not pro-murdering babies.
I'm pro-Becky who found out at her 20 week anatomy scan that the infant she had been so excited to bring into this world had developed without life sustaining organs.
HEALTH
James Salazar
James Salazar
@JamesSalazarMD
In medicine, reckoning with racism includes reappraising the very syntax we use every day. Proud to add my voice w/ @J_Ikeme and @RWGrantMD in this @JAMAInternMed pub addressing:

Does race/ethnicity belong in the first line of the patient

Some background: I’ve struggled with this question since early in medical school

Medical syntax is designed to communicate information in a predictable sequence with key elements prioritized to facilitate efficient communication and formation of an assessment and plan

2/

From preclinical lectures to Qbank questions to clerkship rotations, race/ethnicity was often prioritized in the same sentence as age + gender.

I grew accustomed to reading/hearing: a 70-year-old Black man w/ history of x, a 50-year-old Hispanic woman presented w/ y.

3/

However, when it came time for me to use race/ethnicity, there was always tension. Race/ethnicity are self/socially-ascribed identities that in clinical practice are almost always assumed by providers based on appearance. I was also concerned about the potential for bias

4/

I wondered how my own care would be impacted or not impacted by my ethnicity (Hispanic) – I have light skin so I’m not sure if my doctors would even identify me as such – but how would my care be different if I was presented as a 30-year-old Hispanic male?

5/
HEALTH
Advertisement
Ottawa Public Health
Ottawa Public Health
@OttawaHealth
THIS IS A CATCHY & ATTENTION-GRABBING TITLE

Today, the Province will likely announce what zone of the reopening framework we'll shift into as of Tuesday. Whatever is announced, though, doesn't change what we need to do. Why?

Kindly read these 14 tweets & we'll tell you. (1/14)

Fun fact: COVID-19 does not follow us on Twitter. COVID doesn't know, or particularly care, if we're in the Red or Orange zone.

The behaviours of the virus do not depend on the current ‘zone’ of public health restrictions. And, to be perfectly candid, neither should ours. (2/14)

Once upon a time we used to say #WeAreInThisTogether in our messaging. Here's the thing: we are, but we aren't. Not everyone is experiencing this pandemic the same.

Nurses, doctors, paramedics & healthcare workers have experienced things much differently than most of us. (3/14)

Some people have been home & isolated for months, while others haven't been able to stop working.

Business owners & hospitality workers have been on a rollercoaster of openings & closures.

Students, parents, teachers & school staff have had to adapt to going from online (4/14)

to in-person learning (and back again) numerous times.
And this virus has disproportionately affected some groups more than others.

But there's the thing: while our experiences of this pandemic haven't been shared, we do have a shared goal.

And we can reach it together. (5/14)
HEALTH
InspiredTeenTherapy
InspiredTeenTherapy
@SashaLPC
Thrd: Menstruation/Dysphoria

1/ Difficult periods are sometimes the first catalyst for young women becoming alienated from their bodies.

Some have given congratulatory speeches about the vague accomplishment of "becoming a woman."

2/ Others learned about periods through a mundane sex-ed lesson at school. Yet others knew very little about their periods except they are sometimes painful, can be embarrassing, and make activities they’d taken for granted,

3/ like swimming and outdoor play, all-of-a-sudden much more difficult.

When young women hate their periods, they might be told, in a matter-of-fact grumbling way, “well, nobody likes having a period, honey. It’s just a part of life.”

4/ On a personal note, till my early/mid 30s, I knew very little about the menstrual cycle. For me it had always been completely out of sight, out of mind. Once a month, I’d be reminded it exists and I’d have a kind of “oh crap!” moment.

5/ I’d complete the necessary hygiene and try to move on with my life. I was often plowing through various stages of this monthly cycle with little acknowledgement or understanding of how my entire mind, body, and mood was ebbing and flowing. Every month, for years on end.
HEALTH
Landon
Landon
@LandonClost
My uncle passed away from cancer when I was 16 years old.

I’ve since spent 100’s of hours researching how to avoid and fight cancer naturally.

Here’s what I found:

1) Boost your stem cells

Your body slowly regenerates using stem cells.

Foods that promote stem cell growth:

• Seafood & fatty fish
• Berries (black, blue, raspberry)
• Broccoli, cauliflower, brussels sprouts

More stem cells = lower chance of cancer

Fasting is also a viable option for increasing your stem cells.

You could do a 24 hour fast once a week.

Or go extreme like my business partner @taylinsimmonds

And fast for 4-7 days at a time.

I’ll stick with 24 hours tops ;)

2) Hack DNA repair for longevity

To amplify DNA repair:

• Sleep 7+ hours
• Exercise regularly
• Try intermittent fasting

Natural DNA repair prevents your cells from mutating.

Eat foods that amplify DNA repair:

• Greens
• Mangoes
• Greek yogurt

The best cancer cure is prevention.
HEALTH

You May Also Like

Patrick McKenzie
Patrick McKenzie
@patio11
Some people really benefit from hearing advice that everyone knows, for the same reason we keep schools open despite every subject in them having been taught before.

In that spirit, here's some quick Things Many People Find Too Obvious To Have Told You Already.

Your idea is not valuable, at all. All value is in the execution. You think you are an exception; you are not. You should not insist on an NDA to talk about it; nobody serious will engage in contract review over an idea, and this will mark you as clueless.

Technologists tend to severely underestimate the difficulty and expense of creating software, especially at companies which do not have fully staffed industry leading engineering teams ("because software is so easy there, amirite guys?")

Charge more. Charge more still. Go on.

The press is a lossy and biased compression of events in the actual world, and is singularly consumed with its own rituals, status games, and incentives. The news necessarily fails to capture almost everything which happened yesterday. What it says is important usually isn't.

Companies find it incredibly hard to reliably staff positions with hard-working generalists who operate autonomously and have high risk tolerances. This is not the modal employee, including at places which are justifiably proud of the skill/diligence/etc of their employees.
TECH
Simon DeDeo
Simon DeDeo
@SimonDeDeo
"I lied about my basic beliefs in order to keep a prestigious job. Now that it will be zero-cost to me, I have a few things to say."


We know that elite institutions like the one Flier was in (partial) charge of rely on irrelevant status markers like private school education, whiteness, legacy, and ability to charm an old white guy at an interview.

Harvard's discriminatory policies are becoming increasingly well known, across the political spectrum (see, e.g., the recent lawsuit on discrimination against East Asian applications.)

It's refreshing to hear a senior administrator admits to personally opposing policies that attempt to remedy these basic flaws. These are flaws that harm his institution's ability to do cutting-edge research and to serve the public.

Harvard is being eclipsed by institutions that have different ideas about how to run a 21st Century institution. Stanford, for one; the UC system; the "public Ivys".
LIFE
Advertisement
Jaya_Upadhyaya
Jaya_Upadhyaya
@Jayalko1
SRI KUMARIAMMAN, KANYAKUMARI (TN)
#bharatmandir #navratri2021

Created by Maharshi Parasurama and also one among the 108 Shakthi Peethas in the world. The name Kanyakumari stands for Kanya(Virgin) and Kumari(girl).
Devi took this form to vanquish the demon Banasura
@GunduHuDuGa


Once, Banasura(grand son of Mahabali) obtained a boon from Shiva that he could be vanquished only by a virgin.
So, Devi took the form of a kumari and started meditating with the desire to marry Shiva at Suchindram.
Pleased Shiva fixed the midnight hour for marriage with Devi.


Devarshi Narada knew that the marriage would end the chance of killing Banasura. So, he assumed the form of a cock and crowed. Shiva returned back to Suchindram thinking that it was dawn.
Angered, Devi cursed that all food and articles meant for wedding turn into sand and shells


When Banasura heard about Devi’s beauty, he tried to take her by force. Devi, then, killed him and granted the wish of Devas to remain there always protecting them.
The murti of Devi stands with a rosary in hand. Her diamond nose-ring is said to be visible even from the sea.


Once an ancient mariner mistook it for a lighthouse and sailing towards it, his ship wrecked upon the Kanya Kumari rocks. In order to prevent such a tragedy from happening again, the eastern door of the shrine is opened only on five special occasions throughout the year.
ALL
Laurie Voss
Laurie Voss
@seldo
The 2018 State of JavaScript survey is out. They got 20,000 responses and have some delicious, delicious data. I'mma thread in some highlights:

First up: JavaScript flavors. There's TypeScript at 47% adoption, a tad higher than npm's own survey results (which said 46%). npm's survey is coming up again soon and will ask about TypeScript in a lot more detail.


I really, *really* like SoJ's "would not use again" question, which lets people who've abandoned a tech self-identify. This is noticeable in the graph above with Flow users -- 41% of people who've used Flow say they wouldn't use it again.

Now JavaScript frameworks. It's been a full year since npm's survey, so these numbers differ from ours in the directions I expected:
React 65% (vs. 60%)
Vue 29% (vs. 24%)
Ember 5% (vs 4%, I was expecting a bigger rise)

But there's a shocker in here: Angular.


npm's survey had Angular at 40% last year and SoJ has it at either:
- 58% (if you include those who don't want to use it again)
- 24% (if you count only those who like it)
Since npm's question didn't ask if they intend to *continue* using it I think that might explain this.
TECH
Vigilant AFA
Vigilant AFA
@AfaVigilant
One fascist to watch in 2021 is Joseph Charles "Oakman" Golinske of SE MI. He's been a Proud Boy for a couple years, but took a break recently from the group and promotes himself through the "Oak Nation" channel on Telegram.


Most people may be familiar with him as the tall guy in the Proud Boys bridge shot, from their August 17, 2019 attack on Portland, which featured an American Guard bus trying (and failing) to bludgeon antifascists with hammers.


He was also with his g/f at the time (Dominique Tota, left of Tarrio), and that's definitely a twitter account folks will want to block/report because he posts on it.


He's been plenty active at the pro-Covid/anti-mask/ReOpen protests in Lansing MI, seen here with Jerry Wayne and an effigy of Gretchen Whitmer, who his militia friends tried to kidnap and publicly execute.


Outside of the Proud Boys, his solo "career" with Oak Nation features the same misogyny, classism and gateway to far-right domestic terrorism the Proud Boys themselves feature. Here's him peddling oxychlorinque and bragging about harassing service workers.
FOR LATER READ