Okay, here we go.
Neural Volume Rendering for Dynamic Scenes
NeRF has shown incredible view synthesis results, but it requires multi-view captures for STATIC scenes.
How can we achieve view synthesis for DYNAMIC scenes from a single video? Here is what I learned from several recent efforts.
Okay, here we go.
NeRF represents the scene as a 5D continuous volumetric scene function that maps the spatial position and viewing direction to color and density. It then projects the colors/densities to form an image with volume rendering.
Volumetric + Implicit -> Awesome!
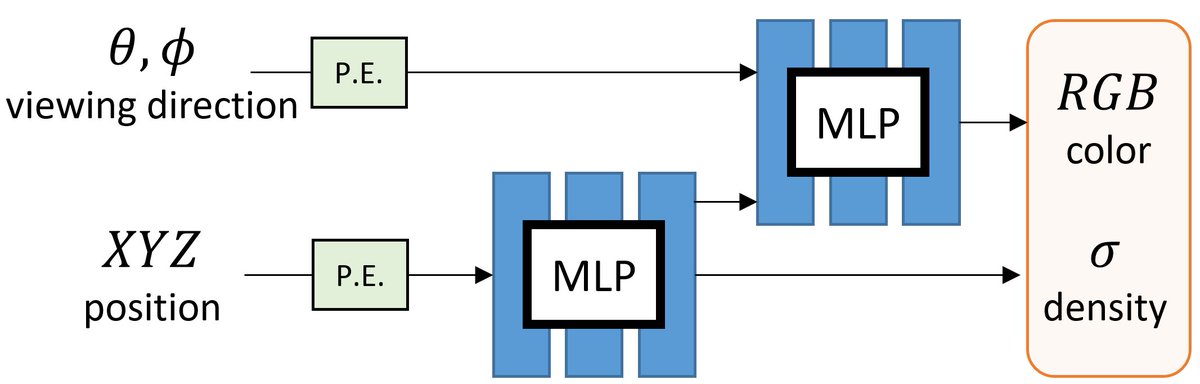
Building on NeRF, one can extend it for handling dynamic scenes with two types of approaches.
A) 4D (or 6D with views) function.
One direct approach is to include TIME as an additional input to learn a DYNAMIC radiance field.
e.g., Video-NeRF, NSFF, NeRFlow
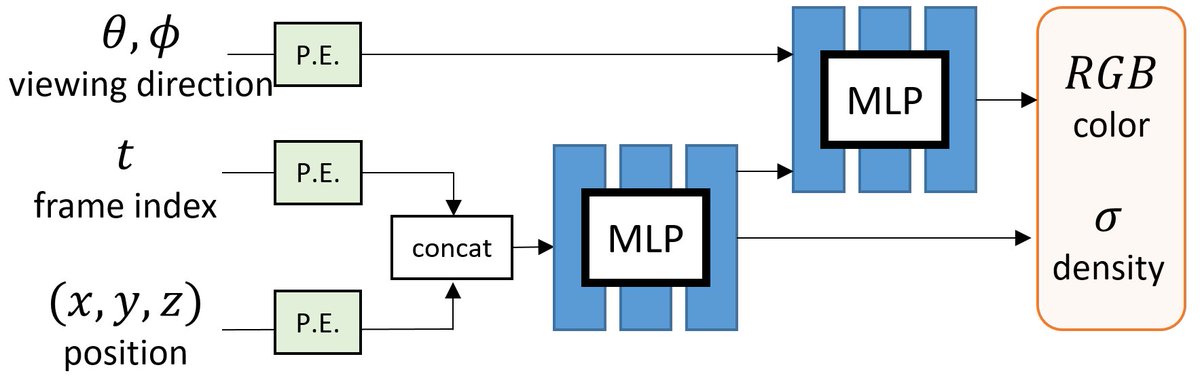
Inspired by non-rigid reconstruction methods, this type of approach learns a radiance field in a canonical frame (template) and predicts deformation for each frame to account for dynamics over time.
e.g., Nerfie, NR-NeRF, D-NeRF
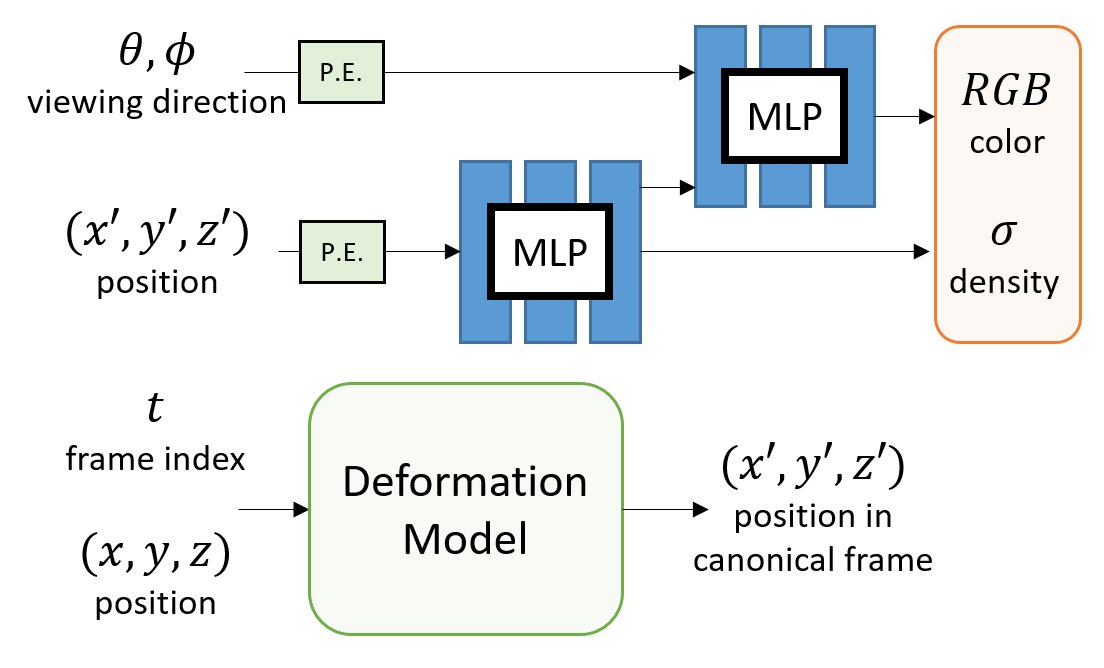
All the methods use an MLP to encode the deformation field. But, how do they differ?
A) INPUT: How to encode the additional time dimension as input?
B) OUTPUT: How to parametrize the deformation field?
One can choose to use EXPLICIT conditioning by treating the frame index t as input.
Alternatively, one can use a learnable LATENT vector for each frame.
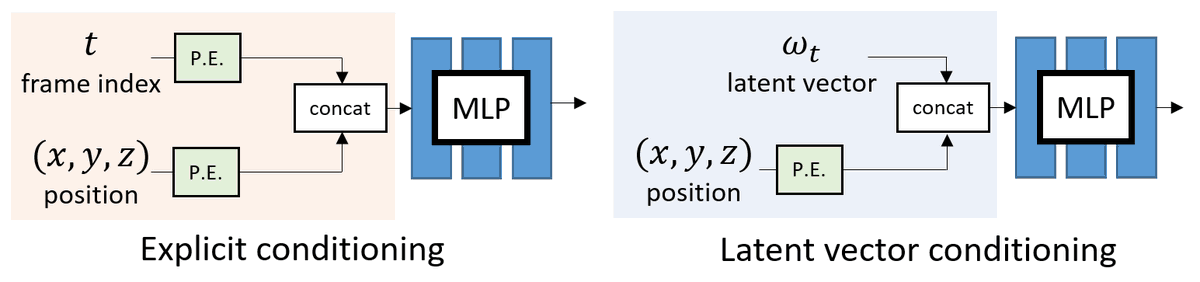
We can either use the MLP to predict
- dense 3D translation vectors (aka scene flow) or
- dense rigid motion field