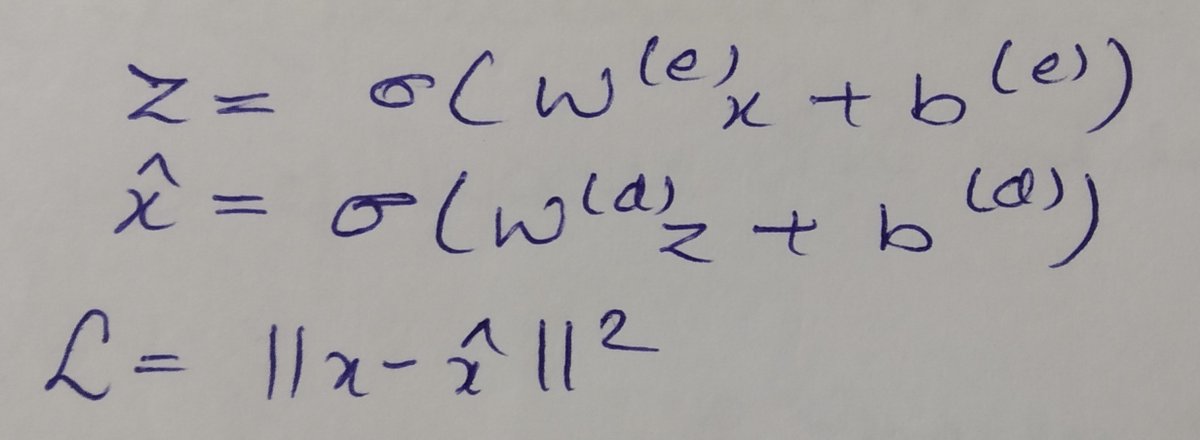Authors Prashant
7 days
30 days
All time
Recent
Popular
Calculating Convolution sizes is something that I found particularly hard after understanding convolutions for the first time.
I couldn't remember the formula because I didn't understand its working exactly.
So here's my attempt to get some intuition behind the calculation.🔣👇
BTW if you haven't read the thread 🧵 on 1D, 2D, 3D CNN, you may want to check it out
First, observe the picture below🖼
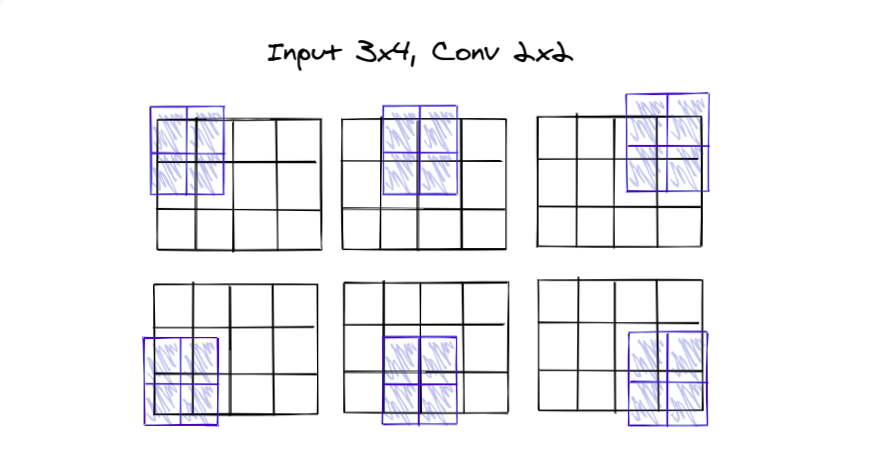
The 2 x 2 filter slides over the
3 rows, 2 times and,
4 columns, 3 times
So, let's try subtracting the filter size first
3 - 2 = 1
4 - 2 = 2
Looks short, we'll need to compensate the 1 in both.
3 - 2 + 1 = 2
4 - 2 + 1 = 3
hence the formula so far becomes:
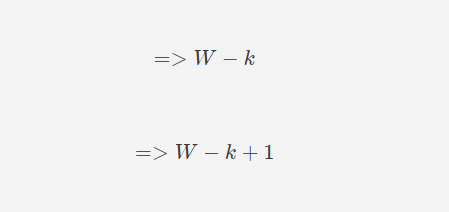
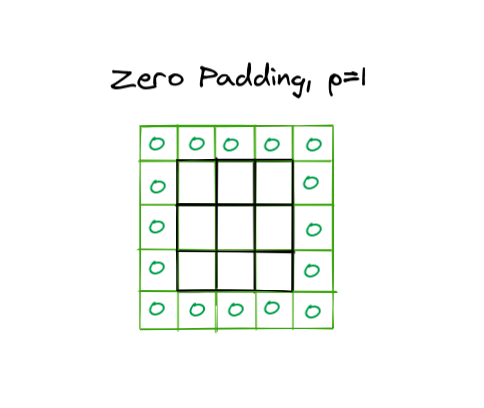
Now let's discuss padding0⃣
Zero padding makes it possible to get output equal to the input by adding extra columns.
It provides extra space for the sliding, making up for the lost space
I couldn't remember the formula because I didn't understand its working exactly.
So here's my attempt to get some intuition behind the calculation.🔣👇

BTW if you haven't read the thread 🧵 on 1D, 2D, 3D CNN, you may want to check it out
Convolutions! 1D! 2D! 3D!\U0001f532
— Prashant (@capeandcode) April 14, 2021
I've had a lot of trouble understanding different convolutions
What do different convolutions do anyway\u2753
Without the correct intuition, I found defining any CNN architecture very unenjoyable.
So, here's my little understanding (with pictures)\U0001f5bc\U0001f447 pic.twitter.com/dCu70j6Ep6
First, observe the picture below🖼

The 2 x 2 filter slides over the
3 rows, 2 times and,
4 columns, 3 times
So, let's try subtracting the filter size first
3 - 2 = 1
4 - 2 = 2
Looks short, we'll need to compensate the 1 in both.
3 - 2 + 1 = 2
4 - 2 + 1 = 3
hence the formula so far becomes:
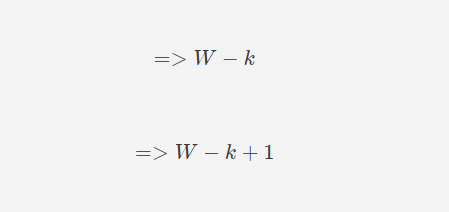
Now let's discuss padding0⃣
Zero padding makes it possible to get output equal to the input by adding extra columns.
It provides extra space for the sliding, making up for the lost space