Alex1Powell Categories Robotics
7 days
30 days
All time
Recent
Popular
Inspired by @michellearning I will be sharing 10 robotics papers that I really enjoyed reading (made me think and raised my heart rate) when I was a grad student. One paper per day. Starting tonight, ending on xmas day. Here we go: 👇🤖 1/n
Note: this is not necessarily an exhaustive list of the best or most influential papers in robotics, nor is it a list of my current favorite papers. These are papers that I found compelling and I still enjoy re-reading from time to time. The order is random. 2/n
[Paper #1] LQR-Trees by Russ Tedrake https://t.co/nYDaHYJryk. I love this paper. It's about feedback control and motion planning with probabilistic guarantees. Given a desired goal state, sample an initial state and find a nominal trajectory from the initial state to the goal 3/n
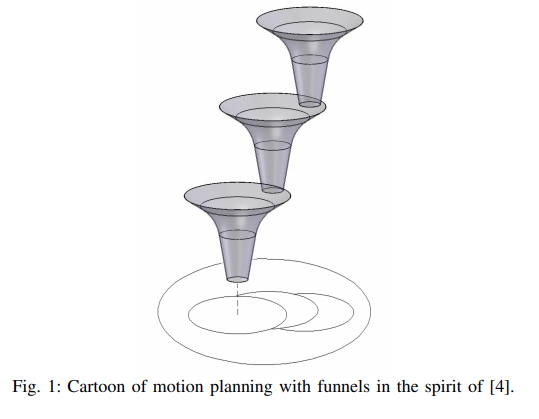
using LQR control (linear dynamics, quadratic cost). So far, so good. Then it gets interesting: it sets out to explicitly compute the region of stability of the computed controller without doing sampling. It underestimates this region by trying to compute a Lyapunov function 4/n
that will certify stability in the region. It only considers Lyapunov functions that are polynomials of deg N and optimizes for a positive function using sums-of-squares programming. So, now you have a nominal trajectory to the goal and a region of stability around it. 5/n
Note: this is not necessarily an exhaustive list of the best or most influential papers in robotics, nor is it a list of my current favorite papers. These are papers that I found compelling and I still enjoy re-reading from time to time. The order is random. 2/n
[Paper #1] LQR-Trees by Russ Tedrake https://t.co/nYDaHYJryk. I love this paper. It's about feedback control and motion planning with probabilistic guarantees. Given a desired goal state, sample an initial state and find a nominal trajectory from the initial state to the goal 3/n

using LQR control (linear dynamics, quadratic cost). So far, so good. Then it gets interesting: it sets out to explicitly compute the region of stability of the computed controller without doing sampling. It underestimates this region by trying to compute a Lyapunov function 4/n
that will certify stability in the region. It only considers Lyapunov functions that are polynomials of deg N and optimizes for a positive function using sums-of-squares programming. So, now you have a nominal trajectory to the goal and a region of stability around it. 5/n


